Density matrix implementation of the numerical renormalization group. More...

#include <nrg.h>

Public Member Functions
	NRG (ChainProvider &chainProvider, Broadener &broadener)
	constructs an NRG algorithm instance The Wilson chain is provided by an implementation of the ChainProvider interface. The Broadener is used after diagonalization of the chain and calculation of the density matrix to broaden the representation of various correlation functions as a discrete set of delta peaks into continous functions. More...

	~NRG ()
	destructs the NRG algorithm object and frees all previously allocated memory.

void	configure (config::Configuration &configuration)
	configures the NRG instance with information in the configuration object. More...

double	getU () const
	retrieves the strength of the on-site impurity interaction U More...

void	setU (double U)
	sets the strength of the on-site impurity interaction U More...

double	getEpsF () const
	retrieves the on-site impurity energy $\epsilon_f$ More...

void	setEpsF (double epsF)
	sets the on-site impurity energy $\epsilon_f$ More...

double	getTemperature () const
	retrieves the system temperature T More...

void	setTemperature (double T)
	sets the system temperature T More...

double	getClusterEnergy () const
	returns the cluster energy. More...

void	setClusterEnergy (double clusterEnergy)
	sets the cluster energy to the indicated value. see getClusterEnergy(). More...

double	getEnergyCutOff () const
	returns the high energy cut-off for state truncation More...

void	setEnergyCutOff (double energyCutOff)
	sets the high energy cut-off for state truncation More...

int	getMaxHilbertSpaceDimension ()
	returns the maximum allowed size of the HilberSpace. See truncateStates(int n). More...

void	setMaxHilbertSpaceDimension (int maxHSdimension)
	sets the maximum allowed size of the HilberSpace. See truncateStates(int n). More...

int	getMaxIterations ()

void	setMaxIterations (int maxIterations)

double	getOccupationUp ()
	returns the exp. value for spin- $\uparrow$ electrons on the impurity. The actual calculation is performed in createPolesG_Up(int n). More...

double	getOccupationDown ()
	returns the exp. value for spin- $\downarrow$ electrons on the impurity. The actual calculation is performed in createPolesG_Down(int n). More...

double	getOccupation ()
	returns the exp. value for electrons on the impurity. The actual calculation is performed in createPolesG_Up(int n) and createPolesG_Down(int n). More...

double	getMagnetization ()
	returns the exp. value for the magnetization More...

void	init ()
	prepares the NRG instance for the iterative diagonalization. More...

void	setupInitialState ()
	initializes the impurity Hamiltonian $H_0$. More...

void	setupHamiltonian (int iteration)
	iterates over all possible quantum number Q and Sz for iteration N and constructs the Hamiltonian for the corresponding HilbertSubSpace. More...

void	truncateStates (int iteration)
	marks all eigenstates above a cut-off energy $E_c$ as discarded. More...

void	propagateLocalMatrixElementUp (int iteration)
	calculates the local impurity matrix elements or spin- $\uparrow$ for a given iteration. More...

void	propagateLocalMatrixElementDown (int iteration)
	see propagateLocalMatrixElementUp(int iteration). This is the spin- $\downarrow$ version. More...

void	propagateLocalMatrixElementUp2 (int iteration)
	calculates other local impurity matrix elements or spin- $\uparrow$ for a given iteration. More...

void	propagateLocalMatrixElementDown2 (int iteration)
	see propagateLocalMatrixElementUp2(int iteration). This is the spin- $\downarrow$ version. More...

void	propagateChainOperatorElementsUp (int iteration)
	calculates the chain matrix elements for spin- $\uparrow$ for a given iteration. More...

void	propagateChainOperatorElementsDown (int iteration)
	see propagateChainOperatorElementsUp(int iteration). This is the spin- $\downarrow$ version. More...

void	createPolesG_Up (int iteration)
	calculates delta peaks for the spin- $\uparrow$ impurity Green's function. More...

void	createPolesG_Down (int iteration)
	see createPolesG_Up(int iteration). This is the spin- $\downarrow$ version. More...

void	createPolesF_Up (int iteration)
	calculates delta peaks for the spin- $\uparrow$ impurity correlator used in the self-energy trick. More...

void	createPolesF_Down (int iteration)
	see createPolesF_Down(int iteration). This is the spin- $\downarrow$ version. More...

void	solve (bool silent=false)
	solves the impurity problem. More...

void	solve_symmetric_SZ (bool silent=false)
	Version of solve(bool silent) for a Wilson chain with Sz symmetry. More...

void	builDM ()
	performs a backward run to construct the reduced density matrices

void	showInfo ()
	lists the physical and numerical parameters for the NRG instance. Also dumps info about the Broadener object.

void	deleteChainOperatorElements (int iteration)
	deletes all chain operator matrix elements for the indicated iteration. More...

void	deleteTransformationMatrices (int iteration)
	deletes all transformation matrices for the indicated iteration. More...

void	deleteDensityMatrices (int iteration)
	deletes all chain operator matrix elements for the indicated iteration. More...

void	deleteImpurityMatrixElements (int iteration)
	deletes all impurity operator matrix elements for the indicated iteration. More...

void	getSelfEnergy (math::CFunction &SUp, math::CFunction &SDown)
	returns the impurity selfenergy. More...

void	getSelfEnergy (math::CFunction &S)
	returns the impurity selfenergy. More...

void	getGreensFunction (math::CFunction &GUp, math::CFunction &GDown)
	returns the impurity Green's function. More...

void	getGreensFunction (math::CFunction &G)
	returns the Green's function. More...

void	getFFunction (math::CFunction &FUp, math::CFunction &FDown)
	returns the correlator for the self-energy trick More...

void	getFFunction (math::CFunction &F)
	returns the correlator for the self-energy trick More...

Protected Attributes
ChainProvider &	m_chainProvider

Broadener &	m_broadener

Broadener *	m_G_Up

Broadener *	m_G_Down

Broadener *	m_F_Up

Broadener *	m_F_Down

math::CFunction	m_F_S_Up

math::CFunction	m_F_S_Down

math::CFunction	m_F_G_Up

math::CFunction	m_F_G_Down

math::CFunction	m_F_F_Up

math::CFunction	m_F_F_Down

double	m_n_Up

double	m_n_Down

double	m_epsF

double	m_U

double	m_temperature

int	m_maxIterations

std::mathbfor< double >	m_energies

HilbertSpaceTable	m_hilbertSpaces

double	m_clusterEnergy

double	m_energyCutOff

int	m_maxHSdimension

int	m_nFirstTruncated

int	signLME [4]

int	dQ [4]

int	dSz [4]

Detailed Description

Density matrix implementation of the numerical renormalization group.

The Numerical Renormalization Group

The Numerical Renormalization Group (NRG) is one of the standard tools to study correlation effects in quantum impurity models. Here a small interacting subsystem with a small number of degrees of freedom (the impurity) is coupled to a bath of fermions. No restriction exists as to the structure of the impurity subsystem. The bath however must consist of non-interacting fermions.

Logarithmic discretization

At the heart of the NRG lies a logarithmic discretization of the continous conduction electron band. The continuum density of states $\rho(\epsilon)$ is approximated by a discrete set of delta poles. By introducing a discretisation parameter $\Lambda$ Wilson divided the normalised energy range $[-1,1]$ into $2n$ intervals where the $n$th interval (for positive $\epsilon$) extends from $\Lambda^{-(n+1)}$ to $\Lambda^n$. The logarithmic discretisation separates the electron energies into different orders of magnitude where energies close to the Fermi level $k_B T \ll D$ with $D$ the bandwidth, which determine the low temperature properties, are well sampled.

Mapping onto a chain

In order to solve the discretized Hamiltonian iteratively one introduces a set of operators $f_{n\sigma}$ with $n>0$ in such a way that they exhibit only nearest neighbour coupling. The Hamiltonian assumes the structure of a hopping Hamiltonian on a semi-infinite chain, which is often referred to as the Wilson chain.

Iterative diagonalization

The transformations performed so far have rendered a form of the Hamiltonian which is amendable to an iterative diagonalisation procedure. Now one defines a sequence of Hamiltonians $H_N$ with $N \geq 0$. The full discrete Hamiltonian is recovered in the limit $N\to\infty$ as

$ \begin{equation} H = \lim_{N\to\infty} \frac{1}{2} (1+\Lambda^{-1}) D \Lambda^{-(N-1)/2}H_N \end{equation} $

Two successive Hamiltonians in the series are connected by the recursion relation

$ \begin{equation} H_{N+1} = \Lambda^{1/2} H_N + t_N ( f^\dagger_{N \sigma} f_{N+1\sigma} + f^\dagger _{N+1\sigma} f_{N\sigma} ) \end{equation} $

with the initial Hamiltonian in the series containing the impurity itself given by

$ \begin{equation} H_0 = \Lambda^{-\frac{1}{2}} \left[ \tilde{\delta_d} c^\dagger_{d \sigma} c_{d \sigma} + \tilde{\Gamma}^{1/2} ( f^\dagger_{0 \sigma} c_{d\sigma} + \text{h.c.} ) + \tilde{U} ( c_{d \sigma}^\dagger c_{d \sigma} - 1)^2\right] \end{equation} $

In this form the single impurity Anderson model can be efficiently solved on a computer by taking advantage of the renormalisation group character of the above description. One starts with a diagonalisation of $H_0$ which can be easily accomplished numerically. Assuming that we have diagonalised a Wilson chain of length $m$ and that the eigenstates are given by $|\mathbf r;m\rangle$ we construct a product basis for the Wilson chain of length $m+1$ by

$ \begin{equation} |(\mathbf r,\alpha_{m+1});m+1 \rangle = |\mathbf r; m \rangle \otimes |\alpha_{m+1}\rangle \end{equation} $

where $|\alpha_{m+1}\rangle$ are the eigenstates of the decoupled site $|\alpha_{m+1}\rangle=\{ |\rangle,|\uparrow\rangle,|\downarrow\rangle,| \uparrow \downarrow \rangle \}$. The matrix elements of the Hamiltonian for the Wilson chain of length $m+1$ for this product basis are given by

$ \begin{align} \langle(\mathbf r',\alpha'_{m+1}); m+1|&H_{m+1} |(\mathbf r,\alpha_{m+1}); m+1\rangle = \Lambda^{1/2} E_{\mathbf r,m} \delta_{\mathbf r \mathbf r'} \delta_{\alpha \alpha'} \nonumber \\ &+\left( \langle \mathbf r'; m |f^\dagger_{m\sigma} |\mathbf r;m \rangle \langle \alpha' | f_{m+1\alpha} |\alpha \rangle + \langle \mathbf r'; m | f_{m\sigma} |\mathbf r;m \rangle \langle\alpha'| f^\dagger_{m+1\alpha} |\alpha\rangle\right) \end{align} $

The eigenvalue problem for the chain of length $m+1$ can therefore be solved numerically using only a knowledge of the eigenspectrum of the chain of length $m$ and the matrix elements of the operators $f_{m\sigma}^\dagger$. Diagonalising the Hamiltonian $H_{m+1}$, set up in the above product basis, can be described by a unitary transformation

$ \begin{equation} |\mathbf r'; m+1 \rangle = \sum_{\alpha_{m+1}, \mathbf r} U^{\alpha_{m+1}}_{\mathbf r', \mathbf r} |\mathbf r;m\rangle \otimes |\alpha_{m+1}\rangle \end{equation} $

where $|\mathbf r'; m+1 \rangle$ denotes the new eigenbasis of the Hamiltonian $H_{m+1}$.

Illustration of the truncation procedure. The

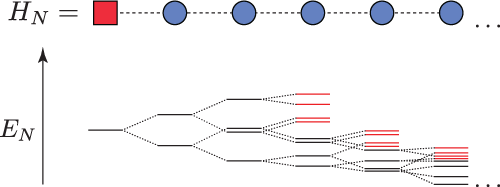
iterative diagonalisation splits each energy level into 4 levels upon the addition of another chain element. In this schematic picture however each energy level is split into only two levels in order not to make the illustration to cluttered. Due to the exponential decrease in the couplings it is save to truncate the high energy states without altering the spectrum of the low energy states. The truncated states are marked red."

References

Constructor & Destructor Documentation

nrg::NRG::NRG	(	ChainProvider &	chainProvider,
		Broadener &	broadener
	)

constructs an NRG algorithm instance The Wilson chain is provided by an implementation of the ChainProvider interface. The Broadener is used after diagonalization of the chain and calculation of the density matrix to broaden the representation of various correlation functions as a discrete set of delta peaks into continous functions.

Parameters

[in]	chainProvider	implementation of the ChainProvider interface; supplies the Wilson chain.
[in]	broadener	implementation of the Broadener interface; broadens the discrete set of delta peaks of the correlation functions into continous functions.

Member Function Documentation

void nrg::NRG::configure ( config::Configuration & configuration )

configures the NRG instance with information in the configuration object.

Parameters

[in] configuration a configuration object which can be queried for various numerical and physical parameters concerning the impurity problem.

void nrg::NRG::createPolesF_Down ( int iteration )

see createPolesF_Down(int iteration). This is the spin- $\downarrow$ version.

Parameters

[in] iteration NRG iteration

void nrg::NRG::createPolesF_Up ( int iteration )

calculates delta peaks for the spin- $\uparrow$ impurity correlator used in the self-energy trick.

This function uses the reduced density matrix and the impurity operator matrix elements to calculate delta peaks of the Lehmann representation of the spin- $\uparrow$ correlator for the given iteration used in the self-energy trick.

Parameters

[in] iteration NRG iteration

void nrg::NRG::createPolesG_Down ( int iteration )

see createPolesG_Up(int iteration). This is the spin- $\downarrow$ version.

Parameters

[in] iteration NRG iteration

void nrg::NRG::createPolesG_Up ( int iteration )

calculates delta peaks for the spin- $\uparrow$ impurity Green's function.

This function uses the reduced density matrix and the impurity operator matrix elements to calculate delta peaks of the Lehmann representation of the spin- $\uparrow$ impurity Green's function for the given iteration.

Parameters

[in] iteration NRG iteration

void nrg::NRG::deleteChainOperatorElements ( int iteration )

deletes all chain operator matrix elements for the indicated iteration.

Parameters

[in] iteration NRG iteration

void nrg::NRG::deleteDensityMatrices ( int iteration )

deletes all chain operator matrix elements for the indicated iteration.

Parameters

[in] iteration NRG iteration

void nrg::NRG::deleteImpurityMatrixElements ( int iteration )

deletes all impurity operator matrix elements for the indicated iteration.

Parameters

[in] iteration NRG iteration

void nrg::NRG::deleteTransformationMatrices ( int iteration )

deletes all transformation matrices for the indicated iteration.

Parameters

[in] iteration NRG iteration

double nrg::NRG::getClusterEnergy ( ) const

inline

returns the cluster energy.

Symmetries create degeneracies in the spectrum of eigenstates. Due to numerical noise these states can energetically drift apart by tiny amounts. It is generally not a good idea to cut-off within a multiplet (or "cluster"). It is ensured that no cut is made in between two energy levels less than a certain energy difference apart. This function returns this energy difference.

Returns: cluster energy

double nrg::NRG::getEnergyCutOff ( ) const

inline

returns the high energy cut-off for state truncation

Returns: high-energy cut-off

double nrg::NRG::getEpsF ( ) const

inline

retrieves the on-site impurity energy $\epsilon_f$

Returns: epsF on-site energy $\epsilon_f$

void nrg::NRG::getFFunction	(	math::CFunction &	FUp,
		math::CFunction &	FDown
	)

inline

returns the correlator for the self-energy trick

Parameters

FUp	reference to spin- $\uparrow$ correlator
FDown	reference to spin- $\downarrow$ correlator

void nrg::NRG::getFFunction ( math::CFunction & F )

inline

returns the correlator for the self-energy trick

Parameters

F	reference to spin- $\uparrow$ correlator

void nrg::NRG::getGreensFunction	(	math::CFunction &	GUp,
		math::CFunction &	GDown
	)

inline

returns the impurity Green's function.

Parameters

[out]	GUp	reference to spin- $\uparrow$ Green's function
[out]	GDown	reference to spin- $\downarrow$ Green's function

void nrg::NRG::getGreensFunction ( math::CFunction & G )

inline

returns the Green's function.

Parameters

[out] G reference to spin- $\uparrow$ Green's function

double nrg::NRG::getMagnetization ( )

inline

returns the exp. value for the magnetization

The actual calculation is performed in createPolesG_Up(int n) and createPolesG_Down(int n). The magnetization is calculated as $ \avg{m} = \avg{n_\uparrow} - \avg{\downarrow}$

Returns

int nrg::NRG::getMaxHilbertSpaceDimension ( )

inline

returns the maximum allowed size of the HilberSpace. See truncateStates(int n).

Returns: max dimension of HilbertSpace

int nrg::NRG::getMaxIterations ( )

inline

returns the number of NRG iterations to be performed.

Returns: NRG iterations

double nrg::NRG::getOccupation ( )

inline

returns the exp. value for electrons on the impurity. The actual calculation is performed in createPolesG_Up(int n) and createPolesG_Down(int n).

Returns

double nrg::NRG::getOccupationDown ( )

inline

returns the exp. value for spin- $\downarrow$ electrons on the impurity. The actual calculation is performed in createPolesG_Down(int n).

Returns

double nrg::NRG::getOccupationUp ( )

inline

returns the exp. value for spin- $\uparrow$ electrons on the impurity. The actual calculation is performed in createPolesG_Up(int n).

Returns

void nrg::NRG::getSelfEnergy	(	math::CFunction &	SUp,
		math::CFunction &	SDown
	)

inline

returns the impurity selfenergy.

Parameters

[out]	SUp	reference to spin- $\uparrow$ self energy
[out]	SDown	reference to spin- $\downarrow$ self energy

void nrg::NRG::getSelfEnergy ( math::CFunction & S )

inline

returns the impurity selfenergy.

Parameters

[out] S reference to spin- $\uparrow$ self energy

double nrg::NRG::getTemperature ( ) const

inline

retrieves the system temperature T

Returns: system temperature T

double nrg::NRG::getU ( ) const

inline

retrieves the strength of the on-site impurity interaction U

Returns: on-site impurity interaction U

void nrg::NRG::init ( )

prepares the NRG instance for the iterative diagonalization.

The function performs the following steps:

Initialization

If the max. iterations have not been set, chooses them automatically based on the system temperature T.
Checks whether enough NRG iteration will be performed for the given temperature T.
Calls the ChainProvider to prepare a chain of the appropriate length,
Sets the temperature T in the broadeners and initializes them.
Calls setupInitialState() to initialize the impurity Hamiltonian $H_0$.

void nrg::NRG::propagateChainOperatorElementsDown ( int iteration )

see propagateChainOperatorElementsUp(int iteration). This is the spin- $\downarrow$ version.

Parameters

[in] iteration NRG iteration

void nrg::NRG::propagateChainOperatorElementsUp ( int iteration )

calculates the chain matrix elements for spin- $\uparrow$ for a given iteration.

Assuming that we have diagonalised a Wilson chain of length $m$ and that the eigenstates are given by $|\mathbf r;m\rangle$ we construct a product basis for the Wilson chain of length $m+1$ by

$ \begin{equation} |(\mathbf r,\alpha_{m+1});m+1\rangle = |\mathbf r; m\rangle \otimes |\alpha_{m+1}\rangle \end{equation} $

where $|\alpha_{m+1}\rangle$ are the eigenstates of the decoupled site $|\alpha_{m+1}\rangle=\{ |\rangle,|\uparrow\rangle,|\downarrow\rangle,| \uparrow \downarrow \rangle \}$. The matrix elements of the Hamiltonian for the Wilson chain of length $m+1$ for this product basis are given by

$ \begin{align} \langle(\mathbf r',\alpha'_{m+1}); m+1| &H_{m+1} |(\mathbf r,\alpha_{m+1}); m+1\rangle = \Lambda^{1/2} E_{\mathbf r,m} \delta_{\mathbf r \mathbf r'} \delta_{\alpha \alpha'} \nonumber \\ &+\left( \langle \mathbf r'; m | f^\dagger_{m\sigma} | \mathbf r;m \rangle \langle \alpha'| f_{m+1\alpha} |\alpha \rangle + \langle \mathbf r'; m | f_{m\sigma} |\mathbf r;m\rangle \langle\alpha'| f^\dagger_{m+1\alpha} |\alpha\rangle\right). \end{align} $

It is precisely the matrix elements $ \langle \mathbf r'; m | f^\dagger_{m\uparrow} | \mathbf r;m \rangle $, which are calculated in this function.

Parameters

[in] iteration NRG iteration

void nrg::NRG::propagateLocalMatrixElementDown ( int iteration )

see propagateLocalMatrixElementUp(int iteration). This is the spin- $\downarrow$ version.

Parameters

[in] iteration NRG iteration

void nrg::NRG::propagateLocalMatrixElementDown2 ( int iteration )

see propagateLocalMatrixElementUp2(int iteration). This is the spin- $\downarrow$ version.

Parameters

[in] iteration NRG iteration

void nrg::NRG::propagateLocalMatrixElementUp ( int iteration )

calculates the local impurity matrix elements or spin- $\uparrow$ for a given iteration.

Lehmann resolving the impurity spectral function one obtains

$ \begin{equation} A_\sigma(\omega) = \sum_{a,b} \bra{b} c_{d\sigma}\ket{a} \frac{\exp{\left[ -\beta E_a \right]}}{Z} \bra{a}c_{d\sigma}^\dagger\ket{b} \delta(\omega + E_a - E_b) \end{equation} $

where $Z$ is the total partition function $Z = {[ - E_a ]}$, ${a}$ and ${b}$ are a complete set of states and $E_a$ is the eigenenergy of state ${a}$. We see that the Lehmann representation gathers the necessary information to construct the spectrum from knowledge of certain matrix elements encoding hopping processes between the impurity and the conduction electron band. It is precisely these matrix elements $ \langle \mathbf r'; m | c^\dagger_{\uparrow} | \mathbf r;m \rangle \delta_{\alpha' \alpha} $ which are calculated in this function.

Parameters

[in] iteration NRG iteration

void nrg::NRG::propagateLocalMatrixElementUp2 ( int iteration )

calculates other local impurity matrix elements or spin- $\uparrow$ for a given iteration.

Bulla et al. first showed that it is possible to write the self-energy as the ratio of two correlation functions, both of which can be calculated directly within the NRG. An equation of motion technique is used to show that the self-energy is given by,

$ \begin{equation} \Sigma_\sigma(\omega) = U \frac{F_{\sigma}(\omega)}{G_{\sigma}(\omega)} \end{equation} $

where $G_{}()$ is the impurity Green's function defined as

$ \begin{equation} G_{\sigma}(\omega) = -i \int_{-\infty}^\infty dt~e^{ i \omega t } \Theta(t) \avg{ \left\{ f_{\sigma}(t), f_{\sigma}^\dagger \right\} } \end{equation} $

and $F_{}()$ is an auxiliary correlation function given by

$ \begin{equation} F_{\sigma}(\omega) = -i \int_{-\infty}^\infty dt e^{ i \omega t } \Theta(t) \avg{ \left\{ \left( f_{\bar{\sigma}}^\dagger f_{\bar{\sigma}} f_{\sigma}\right)(t), f_{\sigma}^\dagger \right\} } \end{equation} $

The imaginary parts of $F_{}()$ and $G_{}()$ are calculated from NRG data using the Lehman sum within the full density matrix approach, with the poles of the spectrum broadened as above. The real parts are then obtained by Kramers-Kronig transform. Discretization artifacts cancel to some extent by dividing the two quantities. This produces a rather smooth self-energy, which in term can be used to calculate an improved spectrum for the impurity. Z-averaging can also be used to further increase accuracy and resolution.

It is precisely these matrix elements $ \langle \mathbf r'; m | c^\dagger_{\downarrow} c^\phantom{\dagger}_{\downarrow} c^\dagger_{\uparrow} | \mathbf r;m \rangle \delta_{\alpha' \alpha} $ which are calculated in this function.

Parameters

[in] iteration NRG iteration

void nrg::NRG::setClusterEnergy ( double clusterEnergy )

inline

sets the cluster energy to the indicated value. see getClusterEnergy().

Parameters

clusterEnergy

void nrg::NRG::setEnergyCutOff ( double energyCutOff )

inline

sets the high energy cut-off for state truncation

Parameters

[in] clusterEnergy new high-energy cut-off

void nrg::NRG::setEpsF ( double epsF )

inline

sets the on-site impurity energy $\epsilon_f$

Parameters

[in] epsF on-site energy $\epsilon_f$

void nrg::NRG::setMaxHilbertSpaceDimension ( int maxHSdimension )

inline

sets the maximum allowed size of the HilberSpace. See truncateStates(int n).

It is advisable to set this number to a large value (so that it does not get in the way) and let the energy cut-off( see setEnergyCutOff(double energyCutOff) ) do the truncation.

Parameters

[in] maxHSdimension max. dimension of the HilbertSpace

void nrg::NRG::setMaxIterations ( int maxIterations )

inline

sets the number of NRG iterations to be performed.

Parameters

[in] maxIterations # of NRG iterations

void nrg::NRG::setTemperature ( double T )

inline

sets the system temperature T

Parameters

[in] T system temperature T

void nrg::NRG::setU ( double U )

inline

sets the strength of the on-site impurity interaction U

Parameters

U	on-site impurity interaction U

void nrg::NRG::setupHamiltonian ( int iteration )

iterates over all possible quantum number Q and Sz for iteration N and constructs the Hamiltonian for the corresponding HilbertSubSpace.

For a given HilbertSubSpace (HSS) in iteration N the function looks up the appropriate HSSs (up to 4) of iteration N-1 and uses the chain matrix elements to construct the Hamiltonian for the HSS in iteration N. Then the Hamiltonian is diagonalized using a call to Lapack's dsyev Lapack replaces the Hamiltonian m_H in the HSS by the unitary transformation that diagonalized it and places and sorts the eigenvalues (energies) into the HSS object as well. The function discards the chain matrix elements of iteration N-1, which are no longer needed.

Parameters

[in] iteration NRG iteration

void nrg::NRG::setupInitialState ( )

initializes the impurity Hamiltonian $H_0$.

This function creates the first 4 HilbertSubSpace instances for the chain consisting only of the impurity ( $ \{ |\rangle,|\uparrow\rangle,|\downarrow\rangle,| \uparrow \downarrow \rangle \}$ ). It determines the eigenenergies and both the local impurity and the chain matrix elements.

void nrg::NRG::solve ( bool silent = false )

solves the impurity problem.

First, the function queries the ChainProvider whether the provided chain is symmetric with respect to the Sz quantum number. If so, it suffices to calculate all matrix elements and correlator for spin- $\uparrow$ only.

The algorithm moves along the Wilson chain iteratively in a forward-backward- forward pattern.

Step 1 - Forward run: Iterative diagonalization

In the first forward run, the Hamiltonian is iteratively constructed and diagonalized (using setupHamiltonian(int n) ). Chain matrix elements are calculated along the way as needed. Once the highest eigenenergy of the chain exceeds the predefined threshold value, the truncation sets in (see truncateStates(int iteration) ) and only the kept states are used to construct the HilbertSpace of the next iteration.

Step 2 - Backward run: Reduced density matrix

In a second step, buildDM() is called, which performs a backward run starting from the last iteration and calculates the reduced density matrix for the different iterations.

Step 3 - Forward run: Calculation of Correlators

In a third step, a forward run is performed which uses the reduced density matrix to calculate impurity matrix elements. The matrices are propagated from iteration to iteration and used to calculate an approximate Lehmann representation of the impurity Green's function and a another correlation function which is needed for the self-energy trick.

Finally, the discrete set of delta peaks for each correlator is broadened to get continous functions (see Broadener).

Parameters

[in] silent if true, silences the impurity solver (useful for DMFT)

void nrg::NRG::solve_symmetric_SZ ( bool silent = false )

Version of solve(bool silent) for a Wilson chain with Sz symmetry.

Parameters

silent if true, silences the impurity solver (useful for DMFT)

void nrg::NRG::truncateStates ( int iteration )

marks all eigenstates above a cut-off energy $E_c$ as discarded.

The Hilbertspace grows exponentially with the length of the Wilson chain. Therefore the eigenstates have to be truncated above an energy cutoff (see void setEnergyCutOff(double energyCutOff) ). Only the "kept" states in iteration N-1 with an energy smaller than the cut-off are used to construct the Hilbertspace for iteration N. A separation of energy scales is achieved by the logarithmic discretization of the energy band and justifies the truncation: States with a high energy in iteration N-1 cannot affect the structure of the low-energy states in iteration N.

Special attention has to be paid to the role of symmetries. Symmetries create degeneracies in the spectrum of eigenstates. Due to numerical noise these states can energetically drift apart by tiny amounts. It is generally not a good idea to cut-off within a multiplet. It is ensured that no cut is made in between two energy levels less than a certain energy difference apart (see void setClusterEnergy(double clusterEnergy) ).

Parameters

[in] iteration NRG iteration

The documentation for this class was generated from the following files:

/home/chris/Development/Release/NanoStructures/nrg/nrg.h
/home/chris/Development/Release/NanoStructures/nrg/nrg.cpp

FUp	reference to spin- \(\uparrow\) correlator
FDown	reference to spin- \(\downarrow\) correlator

[out]	GUp	reference to spin- \(\uparrow\) Green's function
[out]	GDown	reference to spin- \(\downarrow\) Green's function

[out]	SUp	reference to spin- \(\uparrow\) self energy
[out]	SDown	reference to spin- \(\downarrow\) self energy

Public Member Functions

Protected Attributes

Detailed Description

The Numerical Renormalization Group

Logarithmic discretization

Mapping onto a chain

Iterative diagonalization

References

Constructor & Destructor Documentation

Member Function Documentation

Initialization

Step 1 - Forward run: Iterative diagonalization

Step 2 - Backward run: Reduced density matrix

Step 3 - Forward run: Calculation of Correlators